Qsub quick overview

Introduction

This notebook will show you how to use Qsub to construct structured quantum programs that represents FTQC algorithms. Let's look at how to use Qsub, step by step, in the following order!

• Op and Sub
  • First, we will explain Op and Sub, which represent arbitrary quantum operations in Qsub.
• Standard predefined Ops: qsub.lib.std
  • Next, we will introduce predefined Ops, which is provided in the standard library.
• Resolving Op to Sub
• Compile and analyze a Sub
  • The Sub thus created must be resolved and compiled in order to perform resource estimation and generate quantum circuits for QURI Parts. The following sections describe these resolve and compile processes.
• Custom Op and Sub
  • Users can define their own Op and Sub, which can be used in the same way as predefined Op and Sub. The last section describes how to create such custom Op and Sub.

Op and Sub

In Sub a circuit is represented as a Sub (subroutine) object. A Sub is defined as a sequence of operations on qubits and classical registers.

The most basic thing you can do is to define a Sub using predefined Ops.

from quri_parts.qsub.sub import SubBuilder

# Predefined Ops
from quri_parts.qsub.lib.std import H, CNOT, RZ

# Build a circuit for 2 qubits
b = SubBuilder(2)
q0, q1 = b.qubits
b.add_op(H, (q1,))
b.add_op(CNOT, (q0, q1))
b.add_op(RZ(-0.5), (q1,))
b.add_op(CNOT, (q0, q1))
b.add_op(RZ(0.5), (q1,))
b.add_op(H, (q1,))
sub = b.build()

from quri_parts.qsub.visualize import draw_sub

draw_sub(sub)

Some Ops are parametric: in the above example, RZ is a parametric Op. It is just a function returning a (non-parametric) Op: RZ(0.5) is an Op with the fixed parameter 0.5.

Standard predefined Ops: qsub.lib.std

qsub.lib.std package contains the following standard pre-defined Ops.

from math import pi
from quri_parts.qsub.lib import std

print("Single qubit non-parametric gates:")
for op in [
    std.X,
    std.Y,
    std.Z,
    std.H,
    std.SqrtX,
    std.SqrtXdag,
    std.SqrtY,
    std.SqrtYdag,
    std.S,
    std.Sdag,
    std.T,
    std.Tdag,
]:
    print(" ", op)

print("Single qubit parametric rotation gates:")
for op in [
    std.RX,
    std.RY,
    std.RZ,
    std.Phase,
]:
    print(" ", op(pi/8))

print("Two qubit non-parametric gates:")
for op in [
    std.CNOT,
    std.CZ,
    std.SWAP,
]:
    print(" ", op)

print("Three qubit non-parametric gates:")
print(" ", std.Toffoli)

print("Measurement:")
print(" ", std.M)

print("Classical conditional branching:")
for op in [
    std.Cbz,
    std.Label,
]:
    print(" ", op)


_ = [
    
    "conditional",
    
    "Inverse",
    "Controlled",
    "MultiControlled",
    "scoped_and",
    "scoped_and_clifford_t",
]

Single qubit non-parametric gates:
  lib.std.X(qubits=1, registers=0)
  lib.std.Y(qubits=1, registers=0)
  lib.std.Z(qubits=1, registers=0)
  lib.std.H(qubits=1, registers=0)
  lib.std.SqrtX(qubits=1, registers=0)
  lib.std.SqrtXdag(qubits=1, registers=0)
  lib.std.SqrtY(qubits=1, registers=0)
  lib.std.SqrtYdag(qubits=1, registers=0)
  lib.std.S(qubits=1, registers=0)
  lib.std.Sdag(qubits=1, registers=0)
  lib.std.T(qubits=1, registers=0)
  lib.std.Tdag(qubits=1, registers=0)
Single qubit parametric rotation gates:
  lib.std.RX<0.39269908169872414>(qubits=1, registers=0)
  lib.std.RY<0.39269908169872414>(qubits=1, registers=0)
  lib.std.RZ<0.39269908169872414>(qubits=1, registers=0)
  lib.std.Phase<0.39269908169872414>(qubits=1, registers=0)
Two qubit non-parametric gates:
  lib.std.CNOT(qubits=2, registers=0)
  lib.std.CZ(qubits=2, registers=0)
  lib.std.SWAP(qubits=2, registers=0)
Three qubit non-parametric gates:
  lib.std.Toffoli(qubits=3, registers=0)
Measurement:
  lib.std.M(qubits=1, registers=1)
Classical conditional branching:
  lib.std.Cbz(qubits=0, registers=2)
  lib.std.Label(qubits=0, registers=1)

There are some parametric Ops that take another Op as their argument.

Inverse

Inverse returns inverse of a given unitary operation.

from quri_parts.qsub.lib import std

invS = std.Inverse(std.S)
print(invS)

lib.std.Inverse<lib.std.S>(qubits=1, registers=0)

Controlled

Controlled represents a controlled operation of a given unitary operation. If the given unitary is $n$-qubit operation, then the returned controlled operation is $n+1$-qubit operation; The first qubit is the control qubit.

from quri_parts.qsub.lib import std

ctrlS = std.Controlled(std.S)
print(ctrlS)

ctrlToffoli = std.Controlled(std.Toffoli)
print(ctrlToffoli)

lib.std.Controlled<lib.std.S>(qubits=2, registers=0)
lib.std.Controlled<lib.std.Toffoli>(qubits=4, registers=0)

MultiControlled

MultiControlled represents a multi-bit controlled operation of a given unitary operation. It takes three arguments: the target unitary Op, number of control bits (int) and control value (int). The control value is interpreted by binary representation: e.g. if control_value=0b10100, it is interpreted as bit0=0, bit1=0, bit2=1, bit3=0 and bit4=1.

from quri_parts.qsub.lib import std

mctrlS = std.MultiControlled(std.S, 3, 0b010)
print(mctrlS)

lib.std.MultiControlled<lib.std.S, 3, 2>(qubits=4, registers=0)

Resolving Op to Sub

An Op itself is just an abstract symbol. Eventually it needs to be resolved as either a primitive (native gate) or a Sub. How each Op should be resolved can be registered to a SubRepository, though users usually don't need to be aware of it since we provide a default SubRepository. In order to get a Sub corresponding to an Op, you can use resolve_sub() function. If no correspondence is registered for the given Op, it returns None:

from quri_parts.qsub.resolve import resolve_sub
from quri_parts.qsub.lib import std

subS = resolve_sub(std.S)
print(subS)

None

Most operations in qsub.lib.std are usually treated as primitives, so no correspondence for them is registered by default.

Resolving Inverse

Correspondences for Inverse of standard operations are registered by default.

from math import pi
from quri_parts.qsub.resolve import resolve_sub
from quri_parts.qsub.lib import std

print("Single qubit non-parametric gates:")
for op in [
    std.X,
    std.Y,
    std.Z,
    std.H,
    std.SqrtX,
    std.SqrtXdag,
    std.SqrtY,
    std.SqrtYdag,
    std.S,
    std.Sdag,
    std.T,
    std.Tdag,
]:
    inv = std.Inverse(op)
    inv_sub = resolve_sub(inv)
    print(f" Inverse({op.base_id[1]}): {inv_sub}")

print("Single qubit parametric rotation gates:")
for op in [
    std.RX,
    std.RY,
    std.RZ,
    std.Phase,
]:
    inv = std.Inverse(op(pi/8))
    inv_sub = resolve_sub(inv)
    print(f" Inverse({op.base_id[1]}(pi/8)): {inv_sub}")

print("Two qubit non-parametric gates:")
for op in [
    std.CNOT,
    std.CZ,
    std.SWAP,
]:
    inv = std.Inverse(op)
    inv_sub = resolve_sub(inv)
    print(f" Inverse({op.base_id[1]}): {inv_sub}")

print("Three qubit non-parametric gates:")
inv = std.Inverse(std.Toffoli)
inv_sub = resolve_sub(inv)
print(f" Inverse({std.Toffoli.base_id[1]}): {inv_sub}")

Single qubit non-parametric gates:
 Inverse(X): Sub[lib.std.X(q0)]
 Inverse(Y): Sub[lib.std.Y(q0)]
 Inverse(Z): Sub[lib.std.Z(q0)]
 Inverse(H): Sub[lib.std.H(q0)]
 Inverse(SqrtX): Sub[lib.std.SqrtXdag(q0)]
 Inverse(SqrtXdag): Sub[lib.std.SqrtX(q0)]
 Inverse(SqrtY): Sub[lib.std.SqrtYdag(q0)]
 Inverse(SqrtYdag): Sub[lib.std.SqrtY(q0)]
 Inverse(S): Sub[lib.std.Sdag(q0)]
 Inverse(Sdag): Sub[lib.std.S(q0)]
 Inverse(T): Sub[lib.std.Tdag(q0)]
 Inverse(Tdag): Sub[lib.std.T(q0)]
Single qubit parametric rotation gates:
 Inverse(RX(pi/8)): Sub[lib.std.RX<-0.39269908169872414>(q0)]
 Inverse(RY(pi/8)): Sub[lib.std.RY<-0.39269908169872414>(q0)]
 Inverse(RZ(pi/8)): Sub[lib.std.RZ<-0.39269908169872414>(q0)]
 Inverse(Phase(pi/8)): Sub[lib.std.Phase<-0.39269908169872414>(q0)]
Two qubit non-parametric gates:
 Inverse(CNOT): Sub[lib.std.CNOT(q0, q1)]
 Inverse(CZ): Sub[lib.std.CZ(q0, q1)]
 Inverse(SWAP): Sub[lib.std.SWAP(q0, q1)]
Three qubit non-parametric gates:
 Inverse(Toffoli): Sub[lib.std.Toffoli(q0, q1, q2)]

Resolving Controlled

Correspondences for Controlled of standard operations are registered by default.

from math import pi
from IPython.display import display
from quri_parts.qsub.resolve import resolve_sub
from quri_parts.qsub.visualize import draw_sub
from quri_parts.qsub.lib import std

print("Single qubit non-parametric gates:")
for op in [
    std.X,
    std.Y,
    std.Z,
    std.H,
    std.SqrtX,
    std.SqrtXdag,
    std.SqrtY,
    std.SqrtYdag,
    std.S,
    std.Sdag,
    std.T,
    std.Tdag,
]:
    ctrl = std.Controlled(op)
    ctrl_sub = resolve_sub(ctrl)
    print(f" Controlled({op.base_id[1]}):")
    display(draw_sub(ctrl_sub))

print("Single qubit parametric rotation gates:")
for op in [
    std.RX,
    std.RY,
    std.RZ,
    std.Phase,
]:
    ctrl = std.Controlled(op(pi/8))
    ctrl_sub = resolve_sub(ctrl)
    print(f" Controlled({op.base_id[1]}(pi/8)):")
    display(draw_sub(ctrl_sub))

print("Two qubit non-parametric gates:")
for op in [
    std.CNOT,
    std.CZ,
    std.SWAP,
]:
    ctrl = std.Controlled(op)
    ctrl_sub = resolve_sub(ctrl)
    print(f" Controlled({op.base_id[1]}):")
    display(draw_sub(ctrl_sub))

print("Three qubit non-parametric gates:")
ctrl = std.Controlled(std.Toffoli)
ctrl_sub = resolve_sub(ctrl)
print(f" Controlled({std.Toffoli.base_id[1]}):")
display(draw_sub(ctrl_sub))

Single qubit non-parametric gates:
 Controlled(X):

 Controlled(Y):

 Controlled(Z):

 Controlled(H):

 Controlled(SqrtX):

 Controlled(SqrtXdag):

 Controlled(SqrtY):

 Controlled(SqrtYdag):

 Controlled(S):

 Controlled(Sdag):

 Controlled(T):

 Controlled(Tdag):

Single qubit parametric rotation gates:
 Controlled(RX(pi/8)):

 Controlled(RY(pi/8)):

 Controlled(RZ(pi/8)):

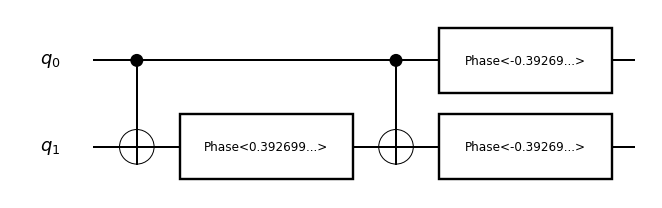
 Controlled(Phase(pi/8)):

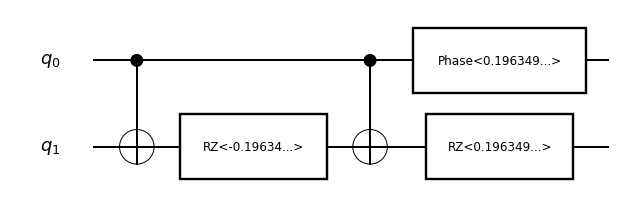
Two qubit non-parametric gates:
 Controlled(CNOT):

 Controlled(CZ):

 Controlled(SWAP):

Three qubit non-parametric gates:
 Controlled(Toffoli):

Resolving MultiControlled

MultiControlled operation is resolved using Toffoli gates by default. (An alternative way to resolve it with measurement and conditional operation is also provided, which will be mentioned elsewhere.) In this construction, if the number of control bits is $k$, then $k-1$ auxiliary qubits are added inside the resolved Sub.

from quri_parts.qsub.resolve import resolve_sub
from quri_parts.qsub.visualize import draw_sub
from quri_parts.qsub.lib import std

mctrlS = std.MultiControlled(std.S, 3, 0b010)
mctrlS_sub = resolve_sub(mctrlS)
draw_sub(mctrlS_sub)

In the above diagram, q4 and q5 are auxiliary qubits added inside the resolved Sub.

Compile and analyze a Sub

By compiling a Sub, you can perform various analysis on the compiled circuit (MachineSub). Let's prepare a Sub to be compiled:

from quri_parts.qsub.sub import SubBuilder
from quri_parts.qsub.visualize import draw_sub
from quri_parts.qsub.lib import std

# Build a circuit for 4 qubits
b = SubBuilder(4)
q0, q1, q2, q3 = b.qubits
b.add_op(std.MultiControlled(std.S, 3, 0b010), (q0, q1, q2, q3))
b.add_op(std.Controlled(std.Sdag), (q2, q1))
sub = b.build()

draw_sub(sub)

In order to perform compilation you need to determine primitives, which specifies which Ops you want to treat as primitives (i.e. not replaced by subroutines). When you are not sure which operations to specify as primitives, you can start with a small set and add missing primitives by inspecting an error message:

from quri_parts.qsub.compile import compile_sub
from quri_parts.qsub.lib import std

primitives = (std.CNOT, std.Toffoli)
try:
    compiled = compile_sub(sub, primitives)
except Exception as e:
    print(e)

Op lib.std.X(qubits=1, registers=0) is not found in calltable.

The error message above tells us that X is missing from primitives. Repeating the procedure, we can come up with the following primitives for this example.

from quri_parts.qsub.compile import compile_sub
from quri_parts.qsub.visualize import draw_msub
from quri_parts.qsub.lib import std

primitives = (std.X, std.T, std.Tdag, std.CNOT, std.Toffoli)
compiled = compile_sub(sub, primitives)
draw_msub(compiled)

Though the circuit diagram is the same as that before the compilation, the compiled subroutine (MachineSub) contains additional information such as definitions of subroutines called internally.

After compilation you can perform several analyses using Evaluator and EvaluatorHooks.

Counting gates in the circuit

You can count gates of specific types in the circuit as follows:

from quri_parts.qsub.evaluate import Evaluator
from quri_parts.qsub.eval import GateCountEvaluatorHooks

gate_counter = Evaluator(GateCountEvaluatorHooks((std.T, std.Tdag, std.Toffoli)))
gate_count = gate_counter.run(compiled)
print({k[1]: v for k, v in gate_count.items()})

{'Toffoli': 4, 'Tdag': 3, 'T': 3}

Counting max number of auxiliary qubits required

Some operations (such as MultiControlled) use auxiliary qubits in addition to input/output qubits of the circuit. you can count the maximum number of simultaneously required auxiliary qubits as follows:

from quri_parts.qsub.evaluate import Evaluator
from quri_parts.qsub.eval import AuxQubitCountEvaluatorHooks

aux_counter = Evaluator(AuxQubitCountEvaluatorHooks())
aux_count = aux_counter.run(compiled)
print(f"Max # of aux qubits: {aux_count}")

Max # of aux qubits: 2

Expand the circuit with primitives

It is possible to expand the circuit with primitives.

from quri_parts.qsub.expand import full_expand
from quri_parts.qsub.visualize import draw_msub

expanded = full_expand(compiled)
draw_msub(expanded)

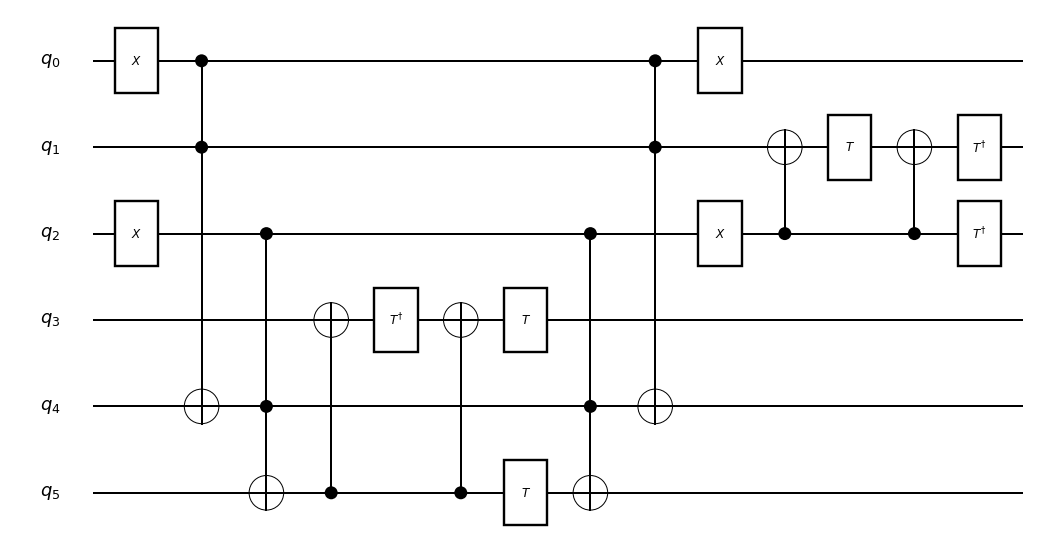
Convert to QURI Parts circuit

You can convert the compiled subroutine to a QURI Parts circuit as follows:

from quri_parts.qsub.evaluate import Evaluator
from quri_parts.qsub.eval import QURIPartsEvaluatorHooks
from quri_parts.circuit.utils.circuit_drawer import draw_circuit

qp_generator = Evaluator(QURIPartsEvaluatorHooks())
qp_circuit = qp_generator.run(compiled)
draw_circuit(qp_circuit, line_length=120)

   ___                                                                             ___                          
  | X |                                                                           | X |                         
--|0  |-----●-------------------------------------------------------●-------------|11 |-------------------------
  |___|     |                                                       |             |___|                         
            |                                                       |              ___     ___     ___     ___  
            |                                                       |             |CX |   | T |   |CX |   |Tdg| 
------------●-------------------------------------------------------●-------------|13 |---|14 |---|15 |---|17 |-
            |                                                       |             |___|   |___|   |___|   |___| 
   ___      |                                                       |     ___       |               |      ___  
  | X |     |                                                       |    | X |      |               |     |Tdg| 
--|1  |-----|-------●---------------------------------------●-------|----|12 |------●---------------●-----|16 |-
  |___|     |       |                                       |       |    |___|                            |___| 
            |       |      ___     ___     ___     ___      |       |                                           
            |       |     |CX |   |Tdg|   |CX |   | T |     |       |                                           
------------|-------|-----|4  |---|5  |---|6  |---|8  |-----|-------|-------------------------------------------
            |       |     |___|   |___|   |___|   |___|     |       |                                           
           _|_      |       |               |               |      _|_                                          
          |TOF|     |       |               |               |     |TOF|                                         
----------|2  |-----●-------|---------------|---------------●-----|10 |-----------------------------------------
          |___|     |       |               |               |     |___|                                         
                   _|_      |               |      ___     _|_                                                  
                  |TOF|     |               |     | T |   |TOF|                                                 
------------------|3  |-----●---------------●-----|7  |---|9  |-------------------------------------------------
                  |___|                           |___|   |___|

Compiling an Op

In the above example, we defined a circuit with 4 input/output qubits as a Sub and compiled it. It is often more convenient if we don't need to specify the required number of qubits explicitly. This is possible by defining your own (parametric) Op and compile it. Defining your own Op will be treated in the next section. Here we illustrate compilation of Op using pre-defined standard Ops.

from quri_parts.qsub.compile import compile
from quri_parts.qsub.visualize import draw_msub
from quri_parts.qsub.lib import std

op = std.MultiControlled(std.S, 3, 0b010)
primitives = (std.X, std.T, std.Tdag, std.CNOT, std.Toffoli)
compiled = compile(op, primitives)
draw_msub(compiled)

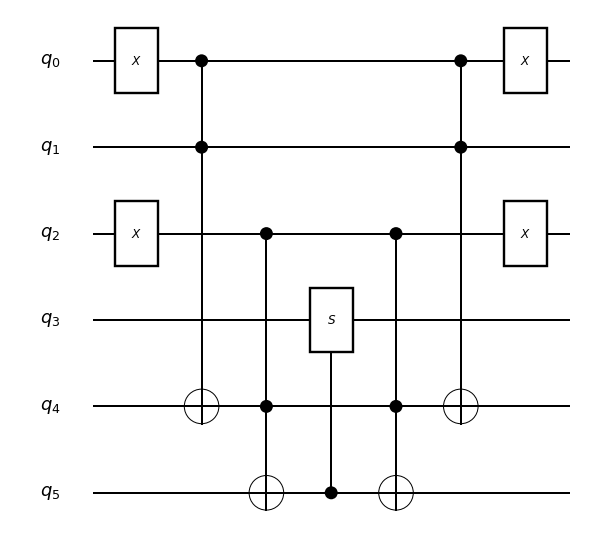
Here you don't need to specify the number of qubits of the Sub (4) as it is automatically calculated by MultiControlled. In this case, the entry Op=MultiControllled<S, 3, 0b010> is resolved to a Sub, so the returned MachineSub is the multi-controlled operation expanded by the default rule. On the other hand, it is not fully expanded and it contains non-primitive Ops such as Controlled<S>.

Custom Op and Sub

With knowledge introduced in the preceding sections, you can build a subroutine (Sub) using pre-defined operations (Op), compile it and analyze the compiled subroutine (MachineSub). The next thing you want to do is probably to use your own subroutine inside another subroutine. It is not possible though; a Sub can contain Ops but not other Subs. In order to call your subroutine from another subroutine, you need to define your own Op along with the Sub and register a corresponding between them.

Defining (non-parametric) Op and Sub

As a simple example, let's define a "majority" operation and its circuit (subroutine).

from quri_parts.qsub.opsub import UnitarySubDef, opsub
from quri_parts.qsub.resolve import resolve_sub
from quri_parts.qsub.visualize import draw_sub
from quri_parts.qsub.lib import std

class MajorityDef(UnitarySubDef):
    name = "Majority"
    qubit_count = 3

    def sub(self, builder):  # builder is a SubBuilder instance
        a, b, c = builder.qubits
        builder.add_op(std.CNOT, (b, a))
        builder.add_op(std.CNOT, (b, c))
        builder.add_op(std.Toffoli, (c, a, b))

Majority, _ = opsub(MajorityDef)

print(Majority)
sub = resolve_sub(Majority)
draw_sub(sub)

__default__.Majority(qubits=3, registers=0)

When defining a unitary Op and corresponding Sub:

• Define a subclass of UnitarySubDef
  • Specify name and qubit_count attributes
  • Implement sub() method that builds the corresponding Sub. A SubBuilder is passed as an argument. Note that you don't need to call builder.build() since it is automatically called later.
• Call opsub() with the defined class (not an instance of the class). The function returns two values:
  • The first return value is the defined Op.
  • The second return value is the defined Sub. You may not need it for the most cases since it is registered to the (default) SubRepository and can be later resolved by resolve_sub().

You can use the defined Op when building another Sub.

from quri_parts.qsub.sub import SubBuilder
from quri_parts.qsub.visualize import draw_sub
from quri_parts.qsub.lib import std

# Build a circuit for 4 qubits
b = SubBuilder(4)
q0, q1, q2, q3 = b.qubits
b.add_op(Majority, (q0, q1, q3))
b.add_op(Majority, (q1, q2, q3))
sub = b.build()

draw_sub(sub)

Defining parametric Op and Sub

You can also define parametric Op and Sub, which can take some parameters.

• Number of input/output qubits can be determined with the parameter values.
• Construction of the Sub can be customized using the parameter values.

We illustrate this by defining "multi-qubit SWAP":

from quri_parts.qsub.opsub import ParamUnitarySubDef, param_opsub
from quri_parts.qsub.resolve import resolve_sub
from quri_parts.qsub.visualize import draw_sub
from quri_parts.qsub.lib import std

class MultiSWAPDef(ParamUnitarySubDef[int]):
    name = "MultiSWAP"

    def qubit_count_fn(self, bits: int):
        return 2 * bits

    def sub(self, builder, bits: int):  # builder is a SubBuilder instance
        x = builder.qubits[:bits]
        y = builder.qubits[bits:]

        for i in range(bits):
            builder.add_op(std.SWAP, (x[i], y[i]))

MultiSWAP, _ = param_opsub(MultiSWAPDef)

print(MultiSWAP(3))
sub = resolve_sub(MultiSWAP(3))
draw_sub(sub)

__default__.MultiSWAP<3>(qubits=6, registers=0)

When defining a parametric unitary Op and corresponding Sub:

• Define a subclass of ParamUnitarySubDef
  • You can specify types of parameters like ParamUnitarySubDef[int]. This is optional; it helps static type checking and can also be considered as documentation.
  • Specify name attribute.
  • If number of input/output qubits is fixed regardless of parameter values, it can be specified with qubit_count attribute.
  • If number of input/output qubits is determined with parameter values, implement qubit_count_fn() method that takes the parameter values and returns the number of qubits.
  • Implement sub() method that takes the parameter values and builds the corresponding Sub. A SubBuilder is passed as the first argument and the parameter values are passed as the other arguments. Note that you don't need to call builder.build() since it is automatically called later.
• Call param_opsub() with the defined class (not an instance of the class). The function returns two values:
  • The first return value is the defined parametric Op. It is a function that takes the parameter values and returns an Op with the parameters substituted.
  • The second return value is the defined parametric Sub. You may not need it for the most cases since it is registered to the (default) SubRepository and can be later resolved by resolve_sub().

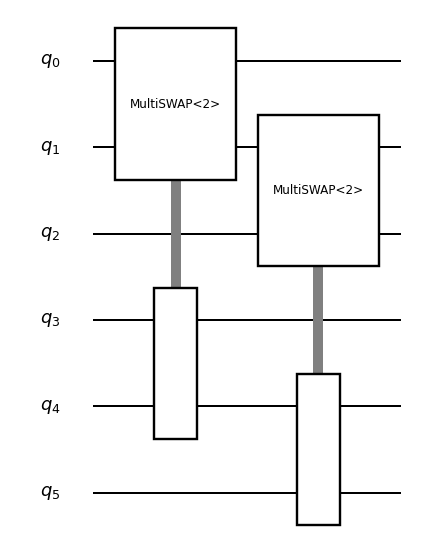
You can use the defined parametric Op when building another Sub.

from quri_parts.qsub.sub import SubBuilder
from quri_parts.qsub.visualize import draw_sub
from quri_parts.qsub.lib import std

# Build a circuit for 6 qubits
b = SubBuilder(6)
q0, q1, q2, q3, q4, q5 = b.qubits
b.add_op(MultiSWAP(2), (q0, q1, q3, q4))
b.add_op(MultiSWAP(2), (q1, q2, q4, q5))
sub = b.build()

draw_sub(sub)

Using with Inverse, Controlled, MultiControlled

User defined Ops can be used in the same way as Ops in the standard library, in combination with Ops in the standard library such as Inverse, Controlled, or MultiControlled. Resolving can be left to the predefined resolver, or if a more efficient resolver is available, it can be registered.

from quri_parts.qsub.lib import std

MCMS = std.MultiControlled(MultiSWAP(2), 3, 0b101)
b = SubBuilder(7)
b.add_op(MCMS, b.qubits)
sub = b.build()

draw_sub(sub)

Summary

As introduced above, Qsub makes it relatively easy to construct complex quantum circuits that represent the FTQC algorithm, perform resource estimation, and generate quantum circuits for QURI Parts. Users can define data structures such as Op and Sub that represent arbitrary quantum operations, which can be combined to form quantum circuits. In addition, commonly used Ops and Subs are predefined and available in the standard library. QURI SDK Enterprize also includes a more advanced library for configuring FTQC algorithms.