Bernstein-Vazirani Algorithm
The Bernstein-Vazirani algorithm is an algorithm that deterministically solves the following problem:
Suppose there is a secret bit string and an oracle that implements the function
Find the secret bit string .
We demonstrate how to use QURI Parts to implement the algorithm.
Building the problem oracle
Now, let's build the quantum circuit that implements the oracle.
from quri_parts.circuit import QuantumCircuit
from quri_parts.circuit.utils.circuit_drawer import draw_circuit
def get_bv_oracle(s: int, bit_length: int) -> QuantumCircuit:
circuit = QuantumCircuit(bit_length + 1)
for i in range(bit_length):
this_s = (s >> i) & 1
if this_s:
circuit.add_CNOT_gate(i, bit_length)
return circuit
As an example, let's assume the secret bit string is and see what the oracle circuit looks like:
draw_circuit(get_bv_oracle(0b1101, 4))
#output
0 ----●-------------------
|
|
|
1 ----|-------------------
|
|
|
2 ----|-------●-----------
| |
| |
| |
3 ----|-------|-------●---
| | |
_|_ _|_ _|_
|CX | |CX | |CX |
4 --|0 |---|1 |---|2 |-
|___| |___| |___|
We may confirm that the oracle we implemented is indeed correct. Let's assume that the secret string is
import numpy as np
from functools import reduce
import pandas as pd
from quri_parts.core.state import ComputationalBasisState
from quri_parts.qulacs.simulator import evaluate_state_to_vector
n_bit_length = 4
n_qubits = n_bit_length + 1
s = 0b1101
oracle = get_bv_oracle(s, 4)
recorder = {}
for i in range(2**n_bit_length):
out_vector = evaluate_state_to_vector(
ComputationalBasisState(n_qubits, bits=i).with_gates_applied(oracle)
).vector
oracle_evaluted = np.where(out_vector)[0][0] >> n_bit_length
expected = reduce(lambda x, y: x^y, [((i & s) >> j) & 1 for j in range(n_bit_length)])
recorder[i] = {"oracle": oracle_evaluted, "expected": expected}
print(pd.DataFrame.from_dict(recorder).to_markdown())
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| oracle | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| expected | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
Given the table above, we have confirmed that the oracle implemention is indeed correct.
Building the Bernstein-Vazirani algorithm circuit
Now, let's build the circuit that implements the Bernstein-Vazirani algorithm. The circuit looks like:
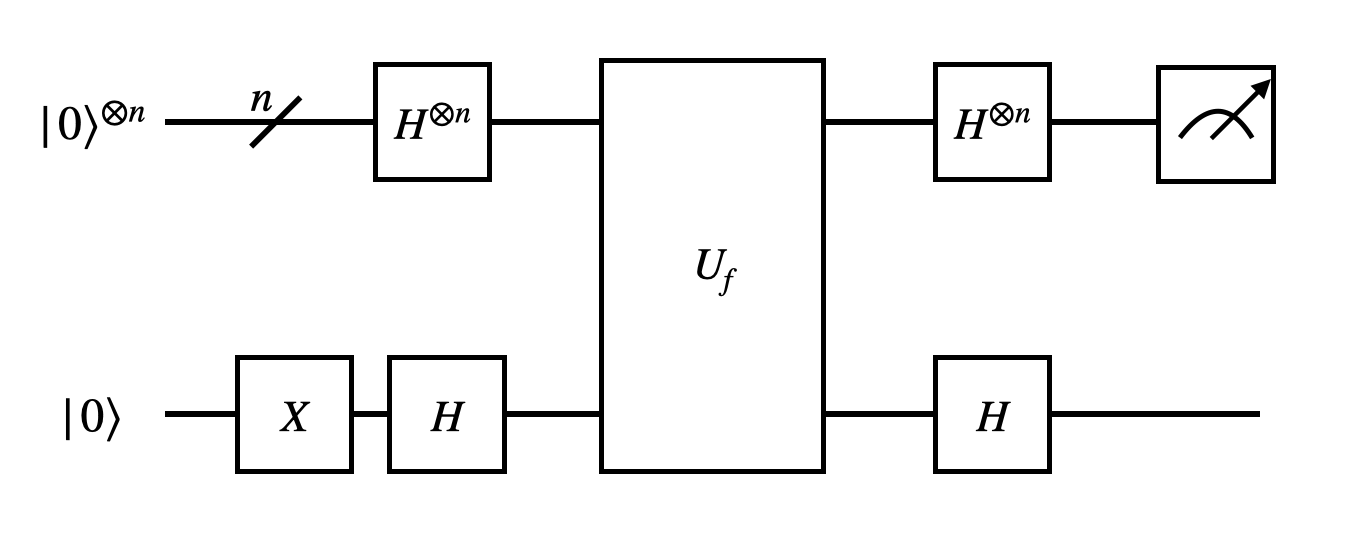
import numpy as np
def get_bv_algorithm_circuit(oracle: QuantumCircuit) -> QuantumCircuit:
bit_length = oracle.qubit_count - 1
circuit = QuantumCircuit(oracle.qubit_count)
circuit.add_X_gate(bit_length)
for i in range(bit_length + 1):
circuit.add_H_gate(i)
circuit.extend(oracle)
for i in range(bit_length + 1):
circuit.add_H_gate(i)
return circuit
Now, let's look at the what the circuit implementing the algorithm looks like.
oracle = get_bv_oracle(0b110101, 6)
draw_circuit(get_bv_algorithm_circuit(oracle))
#output
___ ___
| H | | H |
0 --|1 |-------------��●-----|12 |-------------------------
|___| | |___|
___ ___ |
| H | | H | |
1 --|2 |---|13 |-----|-----------------------------------
|___| |___| |
___ | ___
| H | | | H |
2 --|3 |-------------|-------●-----|14 |-----------------
|___| | | |___|
___ ___ | |
| H | | H | | |
3 --|4 |---|15 |-----|-------|---------------------------
|___| |___| | |
___ | | ___
| H | | | | H |
4 --|5 |-------------|-------|-------●-----|16 |---------
|___| | | | |___|
___ | | | ___
| H | | | | | H |
5 --|6 |-------------|-------|-------|-------●-----|17 |-
|___| | | | | |___|
___ ___ _|_ _|_ _|_ _|_ ___
| X | | H | |CX | |CX | |CX | |CX | | H |
6 --|0 |---|7 |---|8 |---|9 |---|10 |---|11 |---|18 |-
|___| |___| |___| |___| |___| |___| |___|
Finally, let's construct a function that executes the algorithm. As the algorithm is deterministic, it can be executed using a sampler with only 1 shot.
from quri_parts.qulacs.sampler import create_qulacs_vector_sampler
def get_secret_string(oracle: QuantumCircuit, n_shot: int = 1) -> dict[str, int]:
algorithm = get_bv_algorithm_circuit(oracle)
n_qubits = algorithm.qubit_count
sampler = create_qulacs_vector_sampler()
sampling_cnt = sampler(algorithm, n_shot)
get_secret_string_from_int = lambda s: bin(s)[2:].zfill(n_qubits)[1:]
return {get_secret_string_from_int(s): v for s, v in sampling_cnt.items()}
Now, let's execute the algorithm with the secret string fed to the oracle being .
bit_length = 6
s = 0b011101
oracle = get_bv_oracle(s, bit_length)
next(iter(get_secret_string(oracle)))
#output
'011101'
The algorithm indeed gives us the desiresd result as expected.
Showing that the algorithm is deterministic
To ensure the algorithm is indeed deterministic, let's run the circuit 1000 times and see if it gives the exact same result every time.
import seaborn as sns
import matplotlib.pyplot as plt
counts = get_secret_string(oracle, n_shot=1000)
sns.barplot(counts, x=counts.keys(), y=counts.values())
plt.show()
Given that every execution gives the exact same result, we have confirmed that the algorithm is deterministic