メインコンテンツまでスキップ

Quantum gates and circuits

Quantum gates and circuits are essential when working on quantum computing. Here we describe basic treatment of them in QURI Parts.

Prerequisite​

QURI Parts modules used in this tutorial: quri-parts-circuit, quri-parts-core, quri-parts-braket, quri-parts-cirq, quri-parts-qiskit, quri-parts-qulacs, and quri-parts-tket. You can install them as follows:

!pip install "quri-parts[braket,cirq,qiskit,qulacs,tket]" pylatexenc

QuantumGate object​

In QURI Parts, a quantum gate is represented by a QuantumGate object (more precisely NamedTuple). A QuantumGate contains not only the kind of the gate but also some additional information such as gate parameters and qubits on which the gate acts. You can create gate objects using QuantumGate:

from math import pi
from quri_parts.circuit import QuantumGate

gates = [
    # X gate acting on qubit 0
    QuantumGate("X", target_indices=(0,)),
    # Rotation gate acting on qubit 1 with angle pi/3
    QuantumGate("RX", target_indices=(1,), params=(pi/3,)),
    # CNOT gate on control qubit 2 and target qubit 1
    QuantumGate("CNOT", target_indices=(1,), control_indices=(2,)),
]

for gate in gates:
    print(gate)
QuantumGate(name='X', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=())
QuantumGate(name='RX', target_indices=(1,), control_indices=(), classical_indices=(), params=(1.0471975511965976,), pauli_ids=(), unitary_matrix=())
QuantumGate(name='CNOT', target_indices=(1,), control_indices=(2,), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=())

However it is more convenient to use factory functions:

from quri_parts.circuit import X, RX, CNOT

gates = [
    # X gate acting on qubit 0
    X(0),
    # Rotation gate acting on qubit 1 with angle pi/3
    RX(1, pi/3),
    # CNOT gate on control qubit 2 and target qubit 1
    CNOT(2, 1),
]

for gate in gates:
    print(gate)
QuantumGate(name='X', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=())
QuantumGate(name='RX', target_indices=(1,), control_indices=(), classical_indices=(), params=(1.0471975511965976,), pauli_ids=(), unitary_matrix=())
QuantumGate(name='CNOT', target_indices=(1,), control_indices=(2,), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=())

In QURI Parts single-qubit rotation gates are defined as follows:

RX(θ)=exp⁡(−iθ2X)RY(θ)=exp⁡(−iθ2Y)RZ(θ)=exp⁡(−iθ2Z)\begin{align*} R_X(\theta) &= \exp\left( -i\frac{\theta}{2} X\right) \\ R_Y(\theta) &= \exp\left( -i\frac{\theta}{2} Y\right) \\ R_Z(\theta) &= \exp\left( -i\frac{\theta}{2} Z\right) \\ \end{align*}

where θ\theta is called the angle of the gate.

You can access (but not set) attributes of a gate object:

from quri_parts.circuit import PauliRotation

x_gate = X(0)
print(f"name: {x_gate.name}, target: {x_gate.target_indices}")

rx_gate = RX(1, pi/3)
print(f"name: {rx_gate.name}, target: {rx_gate.target_indices}, angle: {rx_gate.params[0]}")

cnot_gate = CNOT(2, 1)
print(f"name: {cnot_gate.name}, control: {cnot_gate.control_indices}, target: {cnot_gate.target_indices}")

pauli_rot_gate = PauliRotation(target_indices=(0, 1, 2), pauli_ids=(1, 2, 3), angle=pi/3)
print(f"name: {pauli_rot_gate.name}, target: {pauli_rot_gate.target_indices}, pauli_ids: {pauli_rot_gate.pauli_ids}, angle: {pauli_rot_gate.params[0]}")
name: X, target: (0,)
name: RX, target: (1,), angle: 1.0471975511965976
name: CNOT, control: (2,), target: (1,)
name: PauliRotation, target: (0, 1, 2), pauli_ids: (1, 2, 3), angle: 1.0471975511965976

QuantumCircuit object​

You can construct a quantum circuit by specifying the number of qubits used in the circuit as follows:

from quri_parts.circuit import QuantumCircuit

# Create a circuit for 3 qubits
circuit = QuantumCircuit(3)
# Add an already created QuantumGate object
circuit.add_gate(X(0))
# Or use methods to add gates
circuit.add_X_gate(0)
circuit.add_RX_gate(1, pi/3)
circuit.add_CNOT_gate(2, 1)
circuit.add_PauliRotation_gate(target_qubits=(0, 1, 2), pauli_id_list=(1, 2, 3), angle=pi/3)

A QuantumCircuit object has several properties:

print("Qubit count:", circuit.qubit_count)
print("Circuit depth:", circuit.depth)

gates = circuit.gates # .gates returns the gates in the circuit as a sequence
print("# of gates in the circuit:", len(gates))
for gate in gates:
    print(gate)
Qubit count: 3
Circuit depth: 3
# of gates in the circuit: 5
QuantumGate(name='X', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=())
QuantumGate(name='X', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=())
QuantumGate(name='RX', target_indices=(1,), control_indices=(), classical_indices=(), params=(1.0471975511965976,), pauli_ids=(), unitary_matrix=())
QuantumGate(name='CNOT', target_indices=(1,), control_indices=(2,), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=())
QuantumGate(name='PauliRotation', target_indices=(0, 1, 2), control_indices=(), classical_indices=(), params=(1.0471975511965976,), pauli_ids=(1, 2, 3), unitary_matrix=())

QuantumCircuit objects can be combined and extended:

circuit2 = QuantumCircuit(3)
circuit2.add_Y_gate(1)
circuit2.add_H_gate(2)

combined = circuit + circuit2 # equivalent: combined = circuit.combine(circuit2)
print("Combined circuit:\n", combined.gates, "\n")

circuit2 += circuit # equivalent: circuit2.extend(circuit)
print("Extended circuit:\n", circuit2.gates, "\n")

# You can also embed a smaller circuit into a larger one
circuit_larger = QuantumCircuit(5)
circuit_larger.add_X_gate(3)
circuit_smaller = QuantumCircuit(3)
circuit_smaller.add_H_gate(0)
circuit_larger.extend(circuit_smaller)
print("Circuit extended by smaller one:\n", circuit_larger.gates)
Combined circuit:
 (QuantumGate(name='X', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='X', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='RX', target_indices=(1,), control_indices=(), classical_indices=(), params=(1.0471975511965976,), pauli_ids=(), unitary_matrix=()), QuantumGate(name='CNOT', target_indices=(1,), control_indices=(2,), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='PauliRotation', target_indices=(0, 1, 2), control_indices=(), classical_indices=(), params=(1.0471975511965976,), pauli_ids=(1, 2, 3), unitary_matrix=()), QuantumGate(name='Y', target_indices=(1,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='H', target_indices=(2,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=())) 

Extended circuit:
 (QuantumGate(name='Y', target_indices=(1,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='H', target_indices=(2,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='X', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='X', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='RX', target_indices=(1,), control_indices=(), classical_indices=(), params=(1.0471975511965976,), pauli_ids=(), unitary_matrix=()), QuantumGate(name='CNOT', target_indices=(1,), control_indices=(2,), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='PauliRotation', target_indices=(0, 1, 2), control_indices=(), classical_indices=(), params=(1.0471975511965976,), pauli_ids=(1, 2, 3), unitary_matrix=())) 

Circuit extended by smaller one:
 (QuantumGate(name='X', target_indices=(3,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()), QuantumGate(name='H', target_indices=(0,), control_indices=(), classical_indices=(), params=(), pauli_ids=(), unitary_matrix=()))

Mutable and immutable circuit objects​

In the above example, a QuantumCircuit object is first created and then some gates are added to it. Contents (in this case a gate sequence) of the QuantumCircuit object are mutated in-place. Such an object is called a mutable object. A mutable circuit is useful to construct a circuit step-by-step, but mutability is often a cause of a trouble. For example, you may pass a circuit to a function and the function may alter contents of the circuit against your intention:

def get_depth(circuit):
    # This function adds some gates despite its name!
    depth = circuit.depth
    circuit.add_X_gate(0)
    return depth

circuit = QuantumCircuit(2)
circuit.add_Z_gate(0)
circuit.add_H_gate(1)
print("# of gates:", len(circuit.gates))

depth = get_depth(circuit)
print("Circuit depth:", depth)
print("# of gates:", len(circuit.gates))
# of gates: 2
Circuit depth: 1
# of gates: 3

In the above example, the circuit depth of the argument and the circuit depth of the return value are different because of the additional gate operation in the get_depth() function.

This example is rather explicit and easy to avoid, but there are more subtle cases for which it is difficult to find the cause of the trouble. To prevent such a problem, you can use an immutable version (which we often call a frozen version) of the circuit obtained by .freeze():

circuit = QuantumCircuit(2)
circuit.add_Z_gate(0)
circuit.add_H_gate(1)
print("# of gates:", len(circuit.gates))

frozen_circuit = circuit.freeze()

try:
    depth = get_depth(frozen_circuit)
except Exception as e:
    print("ERROR:", e)

print("# of gates:", len(circuit.gates))
# of gates: 2
ERROR: 'quri_parts.rust.circuit.circuit.ImmutableQuantumCi' object has no attribute 'add_X_gate'
# of gates: 2

The frozen version does not have methods to alter its contents, so you can safely use one frozen circuit object in many places.

You can call .freeze() on the frozen version too. In this case, the frozen version itself is returned without copy:

print(frozen_circuit)
frozen_circuit2 = frozen_circuit.freeze()
print(frozen_circuit2)
<quri_parts.rust.circuit.circuit.ImmutableQuantumCircuit object at 0x7f48403373f0>
<quri_parts.rust.circuit.circuit.ImmutableQuantumCircuit object at 0x7f48403373f0>

When you want to copy a circuit so that further modification does not affect the original one, call .get_mutable_copy():

copied_circuit = circuit.get_mutable_copy()
copied_circuit.add_X_gate(0)
print("# of gates in circuit:", len(circuit.gates))
print("# of gates in copied_circuit:", len(copied_circuit.gates))

# You can also copy a frozen circuit
copied_circuit2 = frozen_circuit.get_mutable_copy()
copied_circuit2.add_X_gate(0)
print("# of gates in frozen_circuit:", len(frozen_circuit.gates))
print("# of gates in copied_circuit2:", len(copied_circuit2.gates))
# of gates in circuit: 2
# of gates in copied_circuit: 3
# of gates in frozen_circuit: 2
# of gates in copied_circuit2: 3

Circuit conversion​

QURI Parts provides the circuit converter which generates the circuit object designed for other platforms/SDKs. If you want to get the Qulacs circuit, you can use quri_parts.qulacs.circuit.convert_circuit function.

from quri_parts.qulacs.circuit import convert_circuit
qulacs_circuit = convert_circuit(circuit)
print(qulacs_circuit)

import qulacs
qulacs_state = qulacs.QuantumState(2)
qulacs_circuit.update_quantum_state(qulacs_state)
print(qulacs_state)
*** Quantum Circuit Info ***
# of qubit: 2
# of step : 1
# of gate : 2
# of 1 qubit gate: 2
Clifford  : yes
Gaussian  : no


 *** Quantum State ***
 * Qubit Count : 2
 * Dimension   : 4
 * State vector : 
(0.707107,0)
     (-0,-0)
(0.707107,0)
       (0,0)

The location of such a conversion function of course depends on the SDK/simulator you want to use, but it is typically located at quri_parts.[SDK].circuit.convert_circuit.

Currently, we support converting QURI Parts circuit into:

  • Braket circuit: API
  • Cirq circuit: API
  • Qulacs circuit: API
  • Qiskit circuit: API
  • TKet circuit: API

Circuit visualization​

Sometimes it can be a help if you can see the circuit visually to make sure whether the cirucuit is what you really wanted. Here we shows several ways to do it.

Using QURI Parts​

QURI Parts has the function to display ...Circuit with ASCII Art.

from quri_parts.algo.ansatz import HardwareEfficient
from quri_parts.circuit.utils.circuit_drawer import draw_circuit

hwe_ansatz = HardwareEfficient(4, 2)
draw_circuit(hwe_ansatz)
   ___     ___                     ___     ___                     ___     ___  
  |PRY|   |PRZ|                   |PRY|   |PRZ|                   |PRY|   |PRZ| 
--|0  |---|1  |-------------●-----|11 |---|12 |-------------●-----|22 |---|23 |-
  |___|   |___|             |     |___|   |___|             |     |___|   |___| 
   ___     ___             _|_     ___     ___             _|_     ___     ___  
  |PRY|   |PRZ|           |CZ |   |PRY|   |PRZ|           |CZ |   |PRY|   |PRZ| 
--|2  |---|3  |-----●-----|9  |---|13 |---|14 |-----●-----|20 |---|24 |---|25 |-
  |___|   |___|     |     |___|   |___|   |___|     |     |___|   |___|   |___| 
   ___     ___     _|_             ___     ___     _|_             ___     ___  
  |PRY|   |PRZ|   |CZ |           |PRY|   |PRZ|   |CZ |           |PRY|   |PRZ| 
--|4  |---|5  |---|8  |-----●-----|15 |---|16 |---|19 |-----●-----|26 |---|27 |-
  |___|   |___|   |___|     |     |___|   |___|   |___|     |     |___|   |___| 
   ___     ___             _|_     ___     ___             _|_     ___     ___  
  |PRY|   |PRZ|           |CZ |   |PRY|   |PRZ|           |CZ |   |PRY|   |PRZ| 
--|6  |---|7  |-----------|10 |---|17 |---|18 |-----------|21 |---|28 |---|29 |-
  |___|   |___|           |___|   |___|   |___|           |___|   |___|   |___|

Using other libraries​

If you want to get an image as a different form, you can convert ...Circuit into other format such as qiskit's QuantumCircuit and call the method to draw.

Note that in many cases you should bind circuit parameters before conversion because most of the libraries don't have the concept of ParametricCircuit.

qiskit​

import random

from quri_parts.algo.ansatz import HardwareEfficient
from quri_parts.qiskit.circuit import convert_circuit

hwe_ansatz = HardwareEfficient(4, 2)

# bind random parameters
circuit = hwe_ansatz.bind_parameters(
    [random.random() for _ in range(hwe_ansatz.parameter_count)]
)

qiskit_circuit = convert_circuit(circuit)
#qiskit_circuit.draw()  # default: ASCII art
qiskit_circuit.draw("mpl")

png

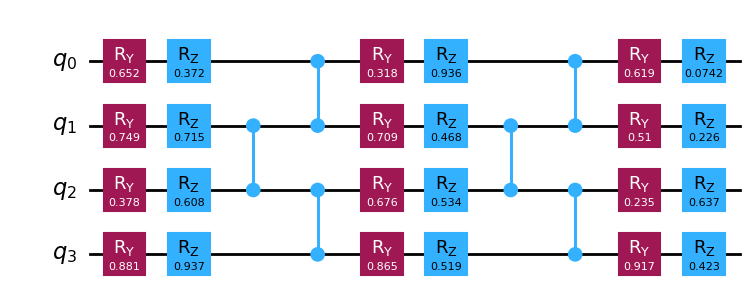
braket​

import random

from quri_parts.algo.ansatz import HardwareEfficient
from quri_parts.braket.circuit import convert_circuit

hwe_ansatz = HardwareEfficient(4, 2)

# bind random parameters
circuit = hwe_ansatz.bind_parameters(
    [random.random() for _ in range(hwe_ansatz.parameter_count)]
)

braket_circuit = convert_circuit(circuit)
print(braket_circuit)
T  : │     0      │     1      │  2  │  3  │     4      │     5      │  6  │  7  │     8      │     9      │
      ┌──────────┐ ┌──────────┐             ┌──────────┐ ┌──────────┐             ┌──────────┐ ┌──────────┐ 
q0 : ─┤ Ry(0.94) ├─┤ Rz(0.82) ├─────────●───┤ Ry(0.07) ├─┤ Rz(0.98) ├─────────●───┤ Ry(0.79) ├─┤ Rz(0.83) ├─
      └──────────┘ └──────────┘         │   └──────────┘ └──────────┘         │   └──────────┘ └──────────┘ 
      ┌──────────┐ ┌──────────┐       ┌─┴─┐ ┌──────────┐ ┌──────────┐       ┌─┴─┐ ┌──────────┐ ┌──────────┐ 
q1 : ─┤ Ry(0.96) ├─┤ Rz(0.91) ├───●───┤ Z ├─┤ Ry(1.00) ├─┤ Rz(0.28) ├───●───┤ Z ├─┤ Ry(0.59) ├─┤ Rz(0.90) ├─
      └──────────┘ └──────────┘   │   └───┘ └──────────┘ └──────────┘   │   └───┘ └──────────┘ └──────────┘ 
      ┌──────────┐ ┌──────────┐ ┌─┴─┐       ┌──────────┐ ┌──────────┐ ┌─┴─┐       ┌──────────┐ ┌──────────┐ 
q2 : ─┤ Ry(0.92) ├─┤ Rz(0.47) ├─┤ Z ├───●───┤ Ry(0.99) ├─┤ Rz(0.92) ├─┤ Z ├───●───┤ Ry(0.09) ├─┤ Rz(0.91) ├─
      └──────────┘ └──────────┘ └───┘   │   └──────────┘ └──────────┘ └───┘   │   └──────────┘ └──────────┘ 
      ┌──────────┐ ┌──────────┐       ┌─┴─┐ ┌──────────┐ ┌──────────┐       ┌─┴─┐ ┌──────────┐ ┌──────────┐ 
q3 : ─┤ Ry(0.66) ├─┤ Rz(0.86) ├───────┤ Z ├─┤ Ry(0.67) ├─┤ Rz(0.21) ├───────┤ Z ├─┤ Ry(0.96) ├─┤ Rz(0.69) ├─
      └──────────┘ └──────────┘       └───┘ └──────────┘ └──────────┘       └───┘ └──────────┘ └──────────┘ 
T  : │     0      │     1      │  2  │  3  │     4      │     5      │  6  │  7  │     8      │     9      │

cirq​

import random

from quri_parts.algo.ansatz import HardwareEfficient
from quri_parts.cirq.circuit import convert_circuit

from cirq.contrib.svg import SVGCircuit

hwe_ansatz = HardwareEfficient(4, 2)

# bind random parameters
circuit = hwe_ansatz.bind_parameters(
    [random.random() for _ in range(hwe_ansatz.parameter_count)]
)

cirq_circuit = convert_circuit(circuit)
# print(cirq_circuit)  # ASCII art
SVGCircuit(cirq_circuit)

svg

tket​

import random

from pytket.circuit.display import render_circuit_jupyter
from quri_parts.algo.ansatz import HardwareEfficient
from quri_parts.tket.circuit import convert_circuit

hwe_ansatz = HardwareEfficient(4, 2)

# bind random parameters
circuit = hwe_ansatz.bind_parameters(
    [random.random() for _ in range(hwe_ansatz.parameter_count)]
)

tket_circuit = convert_circuit(circuit)

render_circuit_jupyter(tket_circuit) # Render interactive circuit diagram